AlphaGOについて書いてある本を読んでいたら、AlphaGOでは入力を黒石の場所、白石の場所、空白の場所の3チャネルに限定しても48%のaccuracyを達成できているということを知った。自分で作ったネットワークでは自分のマークの場所、相手のマークの場所、合法手の場所、置くとローカルボードを取れる場所、置かれるとローカルボードを取られる場所という5つの情報を入力しているにも関わらず(さらに、囲碁よりも手の選択肢が少ないにも関わらず)accuracyは38%程度なので、特徴量を増やす以外にも改善の余地がありそうだと思った。
はじめに、ネットワークをAlphaGOと同じ構成にしてみた。具体的には、以下のように変更した。
class Network(nn.Module):
def forward(self, x):
# AlphaGOと同じ構成
b = F.relu(self.conv1(x))
b = F.relu(self.conv2(b))
b = F.relu(self.conv3(b))
b = F.relu(self.conv4(b))
b = F.relu(self.conv5(b))
b = F.relu(self.conv6(b))
b = F.relu(self.conv7(b))
b = F.relu(self.conv8(b))
b = F.relu(self.conv9(b))
b = F.relu(self.conv10(b))
b = F.relu(self.conv11(b))
b = self.conv12(b)
b = self.conv13(b)
h = b.view(-1, self.channels_num * 81)
h = F.relu(self.fc1(h))
return h
def __init__(self, channels_num):
super(Network, self).__init__()
self.channels_num = channels_num
self.kernel_coef = 30
k = self.kernel_coef * channels_num
self.conv1 = nn.Conv2d(in_channels=channels_num, out_channels=k, kernel_size=(5, 5), padding=(2, 2)).cuda()
self.conv2 = nn.Conv2d(in_channels=k, out_channels=k, kernel_size=(3, 3), padding=(1, 1)).cuda()
self.conv3 = nn.Conv2d(in_channels=k, out_channels=k, kernel_size=(3, 3), padding=(1, 1)).cuda()
self.conv4 = nn.Conv2d(in_channels=k, out_channels=k, kernel_size=(3, 3), padding=(1, 1)).cuda()
self.conv5 = nn.Conv2d(in_channels=k, out_channels=k, kernel_size=(3, 3), padding=(1, 1)).cuda()
self.conv6 = nn.Conv2d(in_channels=k, out_channels=k, kernel_size=(3, 3), padding=(1, 1)).cuda()
self.conv7 = nn.Conv2d(in_channels=k, out_channels=k, kernel_size=(3, 3), padding=(1, 1)).cuda()
self.conv8 = nn.Conv2d(in_channels=k, out_channels=k, kernel_size=(3, 3), padding=(1, 1)).cuda()
self.conv9 = nn.Conv2d(in_channels=k, out_channels=k, kernel_size=(3, 3), padding=(1, 1)).cuda()
self.conv10 = nn.Conv2d(in_channels=k, out_channels=k, kernel_size=(3, 3), padding=(1, 1)).cuda()
self.conv11 = nn.Conv2d(in_channels=k, out_channels=k, kernel_size=(3, 3), padding=(1, 1)).cuda()
self.conv12 = nn.Conv2d(in_channels=k, out_channels=k, kernel_size=(3, 3), padding=(1, 1)).cuda()
self.conv13 = nn.Conv2d(in_channels=k, out_channels=channels_num, kernel_size=(1, 1)).cuda()
self.fc1 = nn.Linear(in_features=channels_num * 9 * 9, out_features=9 * 9).cuda()
この状態で学習を回してみたところ、accuracyは42%程度まで上昇した。
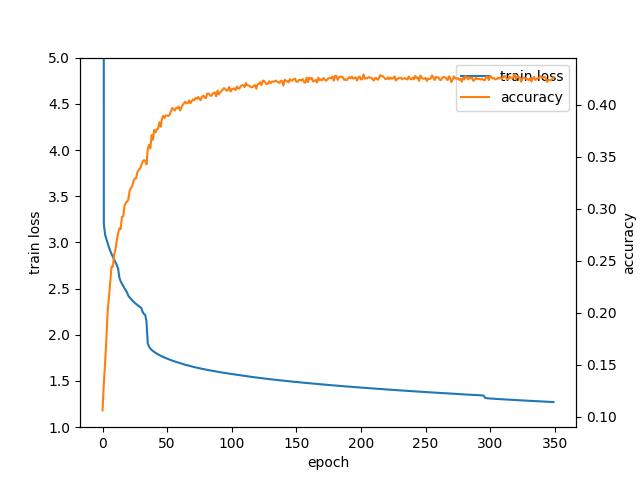
13層のCNN自体は以前にも試したことがあったがこれほど効果があるようには見えなかったので、ReLUを通さない層の存在や最後の全結合層のノード数を変更したことなどが関係あるのだろうか?また、accuracyが最大値に到達したあとに学習を続けると精度が下がっていく動きがなくなった。 また、テストデータの正答率だけではなく訓練データの正答率も測定してみたところ、200エポック付近でテストデータの正答率が上昇しなくなったあとも訓練データに対する正答率は上昇し続けており、350エポック時点ではテストデータの正答率が42.6%であるのに対して訓練データの正答率は56.3%まで到達していることがわかった。
テストデータに対する正答率が上がっていないのに訓練データに対する正答率が上がり続けているということから訓練データに対して過剰に適合していると考えられるので、訓練データが少なすぎるかもしれないと考えて、訓練データを増やしてみることにした。現在MCTS_10000が指した手の情報を合計で50万局面程度用いて学習しているが、これを回転および反転することで訓練データの数を8倍に増やすことができる。具体的には、以下の8種類の並び替えを適用する。
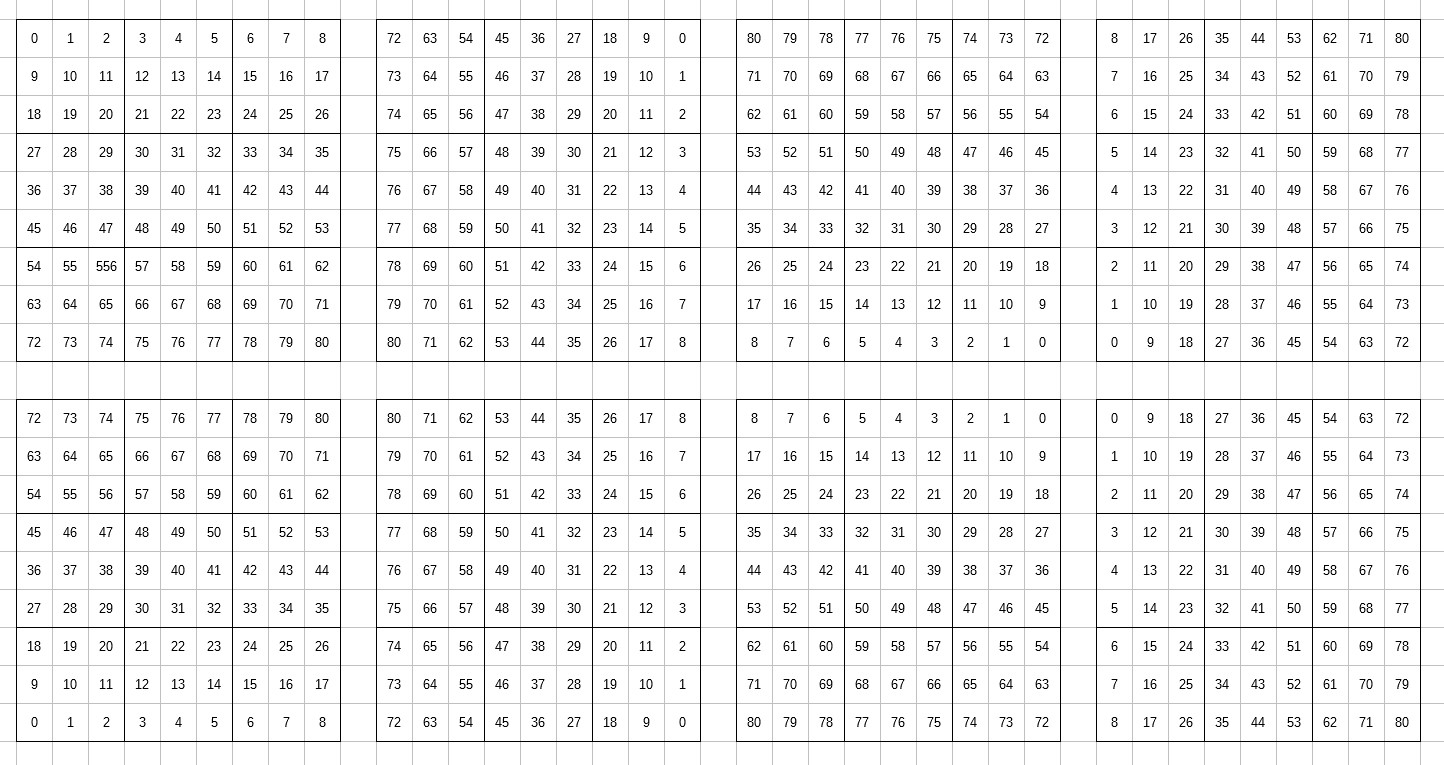
この操作をすることで教師データを400万局面以上に増やすことができた。すると学習の際にデータがメモリに乗らなくなってしまったので、ファイルを8つに分けて10エポックごとに読み込むファイルをローテーションしていくことにした。このようにして学習すると、accuracyの遷移は以下のようになった。
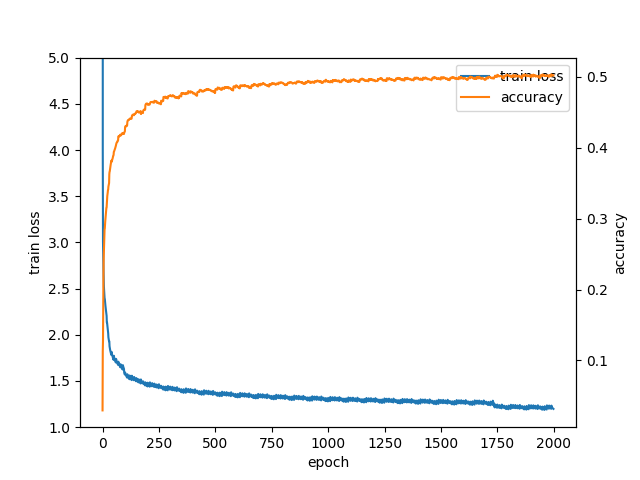
2000エポックほど学習すると正答率は50%に到達し、その状態でもエポック数の増加にともなって正答率は上がり続けているようだった。また、このポリシーを使ってMCTSエージェントと対戦させると、1000プレイアウトのMCTSに対して9割弱、5000プレイアウトのMCTSに対して6割弱の勝率となった。当初は1000プレイアウトのMCTSに勝ち越すことを教師あり学習の目標としていたので、十分達成できただろうと思う。2000エポック時点での訓練データに対する正答率は平均して54%程度あったので、さらに教師データを増やせばもう少し精度をあげられるかもしれないが、教師あり学習は一旦ここまでにして次回からは強化学習を改善していきたい。
戻る