$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
◇◇tech007:座標系45°回転させるやつ◇◇
☆概要
マンハッタン距離を扱う問題は、座標系を$(x,y)$ではなく$(x+y,x-y)$とするとうまくいくことがある。
☆本文
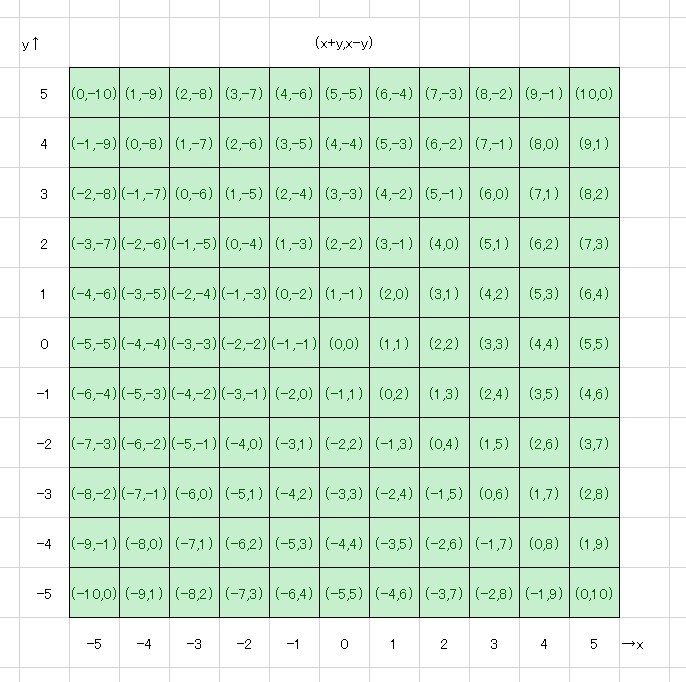
$(x+y,x-y)$という座標系の便利な性質を知ったらここに書いていく
-
座標系$(x,y)$で$(+1,0),(-1,0),(0,+1),(0,-1)$であるような上下左右の移動は、座標系$(x+y,x-y)$では$(+1,+1),(-1,-1),(+1,-1),(-1,+1)$となる。この性質を使えば、2軸を独立に考えられるのでいろいろ便利になる。
-
座標系$(x,y)$でマンハッタン距離が$d$であるような2つの点のペアは、座標系$(x+y,x-y)$ではチェビシェフ距離が$d$であるような2つの点のペアになっている。
☆問題
戻る
